Artificial Intelligence

Last Modified: 4/10/2025

1 Searching

1.1 Agent Design

There are mainly two types of agents: reflex agents and planning agents.

Reflex Agents
- Choose action based on current percept, and may have memory or a model of the world’s current state.
- Do not consider the future consequences of their actions, just consider how the world IS.
Planning Agents
- Decisions based on (hypothesized) consequences of actions.
- Must have a model of how the world evolves in response to actions, and formulate a goal (test), consider how the world WOULD BE.

1.2 Search Problems & Algorithms

A search problem consists of a state space, a successor function (with actions and costs), a start space and a goal test. A solution is a sequence of actions (a plan) which transforms the start state to a goal state.

For a search problem, we may need:

State Space Graph: A mathematical representation of a search problem. It consists of nodes (abstarcted world configurations) and arcs (successors/action results). The goal test is a set of goal nodes (maybe only one).
*Search Trees: A “what if” tree of plans and their outcomes. Nodes show states, and children correspond to successors.

Search algorithms can be divided into two categories:

Uninformed Search: No additional information about states beyond the definition of the problem.
- Depth-First Search
- Breadth-First Search
- Uniform-Cost Search
Informed Search: Use heuristics to guide the search.
- A* Search

1.2.1 Uniform-Cost Search

Uniform-cost search is a variant of Dijkstra’s algorithm. Not inserting all nodes in a graph makes it possible to extend Dijkstra’s algorithm to find the shortest path from a single source to the closest of a set of target nodes on infinite graphs or those too large to represent in memory, which is called uniform-cost search (UCS) in artificial intelligence literature.


105 collapsed lines
1
import java.util.*;
2

3
public class UCS<T> {
4
    private final Map<T, Double> costTo;
5
    private final Map<T, T> parent;
6
    private final PriorityQueue<T> pq;
7
    private final Set<T> visited;
8

9
    /**
10
     * A directed edge constructor with a cost.
11
     */
12
    public static class Edge<T> {
13
        T neighbor;
14
        double cost;
15

16
        public Edge(T neighbor, double cost) {
17
            this.neighbor = neighbor;
18
            this.cost = cost;
19
        }
20
    }
21

22
    /**
23
     * Uniform-cost search constructor.
24
     */
25
    public UCS(Map<T, List<Edge<T>>> graph, T startNode) {
26
        costTo = new HashMap<>();
27
        parent = new HashMap<>();
28
        visited = new HashSet<>();
29

30
        for (T node : graph.keySet()) {
31
            costTo.put(node, Double.POSITIVE_INFINITY);
32
            parent.put(node, null);
33
        }
34
        costTo.put(startNode, 0.0);
35

36
        pq = new PriorityQueue<>(Comparator.comparingDouble(costTo::get));
37
        pq.offer(startNode);
38

39
        while (!pq.isEmpty()) {
40
            T currentNode = pq.poll();
41
            visited.add(currentNode);
42

43
            if (costTo.get(currentNode) == Double.POSITIVE_INFINITY) continue;
44

45
            for (Edge<T> edge : graph.get(currentNode)) {
46
                relax(currentNode, edge.neighbor, edge.cost);
47
            }
48
        }
49
    }
50

51
    /**
52
     * Relaxation of an edge.
53
     *
54
     * @param u the source node
55
     * @param v the target node
56
     * @param cost the cost of the edge
57
     */
58
    private void relax(T u, T v, double cost) {
59
        if (costTo.get(v) > costTo.get(u) + cost) {
60
            costTo.put(v, costTo.get(u) + cost);
61
            parent.put(v, u);
62
            pq.offer(v);
63
        }
64
    }
65

66
    /**
67
     * Get the cost to a node.
68
     *
69
     * @param node the target node
70
     * @return the cost to the target node
71
     */
72
    public double getCostTo(T node) {
73
        return costTo.getOrDefault(node, Double.POSITIVE_INFINITY);
74
    }
75

76
    /**
77
     * Check if a path exists to a node.
78
     *
79
     * @param node the target node
80
     * @return true if a path exists, false otherwise
81
     */
82
    public boolean hasPathTo(T node) {
83
        return costTo.get(node) < Double.POSITIVE_INFINITY;
84
    }
85

86
    /**
87
     * Get the path to a node.
88
     *
89
     * @param targetNode the target node
90
     * @return the path to the target node
91
     */
92
    public List<T> getPathTo(T targetNode) {
93
        if (!hasPathTo(targetNode)) {
94
            return null;
95
        }
96

97
        List<T> path = new ArrayList<>();
98
        for (T v = targetNode; v != null; v = parent.get(v)) {
99
            path.add(v);
100
        }
101

102
        Collections.reverse(path);
103
        return path;
104
    }
105
}


88 collapsed lines
1
#ifndef UCS_H
2
#define UCS_H
3

4
#include <unordered_map>
5
#include <unordered_set>
6
#include <vector>
7
#include <queue>
8
#include <limits>
9
#include <algorithm>
10
#include <functional>
11

12
template <typename T>
13
class UCS {
14
public:
15
    struct Edge {
16
        T neighbor;
17
        double cost;
18

19
        Edge(T neighbor, const double cost) : neighbor(neighbor), cost(cost) {}
20
    };
21

22
private:
23
    std::unordered_map<T, double> costTo;
24
    std::unordered_map<T, T> parent;
25
    std::priority_queue<T, std::vector<T>, std::function<bool(T, T)>> pq;
26
    std::unordered_set<T> visited;
27

28
public:
29
    UCS(const std::unordered_map<T, std::vector<Edge>>& graph, const T& startNode)
30
        : pq([this](T a, T b) { return costTo[a] > costTo[b]; }) {
31

32
        for (const auto& node : graph) {
33
            costTo[node.first] = std::numeric_limits<double>::infinity();
34
            parent[node.first] = T();
35
        }
36
        costTo[startNode] = 0.0;
37

38
        pq.push(startNode);
39

40
        while (!pq.empty()) {
41
            T currentNode = pq.top();
42
            pq.pop();
43
            visited.insert(currentNode);
44

45
            if (costTo[currentNode] == std::numeric_limits<double>::infinity()) continue;
46

47
            for (const auto& edge : graph.at(currentNode)) {
48
                relax(currentNode, edge.neighbor, edge.cost);
49
            }
50
        }
51
    }
52

53
    void relax(const T& u, const T& v, double cost) {
54
        if (costTo[v] > costTo[u] + cost) {
55
            costTo[v] = costTo[u] + cost;
56
            parent[v] = u;
57
            pq.push(v);
58
        }
59
    }
60

61
    double getCostTo(const T& node) const {
62
        auto it = costTo.find(node);
63
        if (it != costTo.end()) {
64
            return it->second;
65
        }
66
        return std::numeric_limits<double>::infinity();
67
    }
68

69
    bool hasPathTo(const T& node) const {
70
        return getCostTo(node) < std::numeric_limits<double>::infinity();
71
    }
72

73
    std::vector<T> getPathTo(const T& targetNode) const {
74
        if (!hasPathTo(targetNode)) {
75
            return {};
76
        }
77

78
        std::vector<T> path;
79
        for (T v = targetNode; v != T(); v = parent.at(v)) {
80
            path.push_back(v);
81
        }
82

83
        std::reverse(path.begin(), path.end());
84
        return path;
85
    }
86
};
87

88
#endif // UCS_H


85 collapsed lines
1
class Edge:
2
    def __init__(self, neighbor, cost):
3
        """
4
        An edge with a neighbor and a cost.
5
        """
6
        self.neighbor = neighbor
7
        self.cost = cost
8

9
class UCS:
10
    def __init__(self, graph, start_node):
11
        """
12
        Initialize uniform-cost search with a graph and a start node.
13
        'graph' is a dict mapping each node to a list of Edge objects.
14
        """
15
        self.cost_to = {}
16
        self.parent = {}
17
        self.visited = set()
18
        self.adj = graph
19

20
        # Initialize all costs to infinity and parents to None
21
        for node in graph:
22
            self.cost_to[node] = float('inf')
23
            self.parent[node] = None
24

25
        # Start node cost is 0
26
        self.cost_to[start_node] = 0.0
27

28
        # Use a list for priority queue (heapq) instead of PriorityQueue
29
        import heapq
30
        self.pq = []
31
        heapq.heappush(self.pq, (0.0, start_node))
32

33
        # Main loop
34
        while self.pq:
35
            current_cost, current_node = heapq.heappop(self.pq)
36
            if current_node in self.visited:
37
                continue
38

39
            self.visited.add(current_node)
40

41
            # Skip if unreachable
42
            if self.cost_to[current_node] == float('inf'):
43
                continue
44

45
            # Relax edges of current node
46
            for edge in self.adj.get(current_node, []):
47
                self.relax(current_node, edge.neighbor, edge.cost)
48

49
    def relax(self, u, v, cost):
50
        """
51
        Update cost_to[v] (relaxation) if a cheaper path is found.
52
        """
53
        new_cost = self.cost_to[u] + cost
54
        if new_cost < self.cost_to[v]:
55
            self.cost_to[v] = new_cost
56
            self.parent[v] = u
57
            import heapq
58
            heapq.heappush(self.pq, (new_cost, v))
59

60
    def get_cost_to(self, node):
61
        """
62
        Get the cost of the path to 'node'.
63
        """
64
        return self.cost_to.get(node, float('inf'))
65

66
    def has_path_to(self, node):
67
        """
68
        Check if a path to 'node' exists.
69
        """
70
        return self.get_cost_to(node) < float('inf')
71

72
    def get_path_to(self, target_node):
73
        """
74
        Reconstruct the path to 'target_node'.
75
        Returns None if no path exists.
76
        """
77
        if not self.has_path_to(target_node):
78
            return None
79

80
        path = []
81
        current = target_node
82
        while current is not None:
83
            path.append(current)
84
            current = self.parent[current]
85
        return path[::-1]

1.2.2 A* Search

A* search is a kind of heuristic search algorithms. It combines uniform-cost search and greedy algorithm.

$g\left(n\right)$ : The cost of the path from the start node to $n$ , which uniform-cost search relies on (path cost).
$h\left(n\right)$ : A heuristic function that estimates the cost of the cheapest path from $n$ to the goal, which greedy algorithm relies on (goal proximity).

The A* search algorithm uses the following formula to calculate the cost of a node:

f\left(n\right) = g\left(n\right) + h\left(n\right)

A heuristic $h$ is admissible (optimistic) if:

h\left(n\right) \leq h^*\left(n\right)

where $h^*\left(n\right)$ is the true cost to reach the goal from node $n$ .

The admissible heuristic guarantees that A* will never stop exploring a path that could lead to a better solution. With inadmissible heuristics, A* may think a node is “too expensive” and stop exploring it, even if that node is actually on the optimal path.

For admissible heuristics, there are some methods for calculating $h\left(n\right)$ :

Manhattan Distance: The sum of the absolute differences of the $x$ and $y$ coordinates.

h\left(n\right) = \left|x_{\text{goal}} - x_{\text{current}}\right| + \left|y_{\text{goal}} - y_{\text{current}}\right|

Euclidean Distance: The straight-line distance between two points.

h\left(n\right) = \sqrt{\left(x_{\text{goal}} - x_{\text{current}}\right)^2 + \left(y_{\text{goal}} - y_{\text{current}}\right)^2}

Chebyshev Distance: The maximum of the absolute differences of the $x$ and $y$ coordinates.

h\left(n\right) = \max\left(\left|x_{\text{goal}} - x_{\text{current}}\right|, \left|y_{\text{goal}} - y_{\text{current}}\right|\right)

Octile Distance: The diagonal distance between two points.

h\left(n\right) = \left(\sqrt{2} - 1\right) \cdot \min\left(\left|x_{\text{goal}} - x_{\text{current}}\right|, \left|y_{\text{goal}} - y_{\text{current}}\right|\right) + \max\left(\left|x_{\text{goal}} - x_{\text{current}}\right|, \left|y_{\text{goal}} - y_{\text{current}}\right|\right)

Zero Heuristic: The heuristic that always returns zero, which makes it the same as uniform-cost search.

Properties

Admissibility: A search algorithm is said to be admissible if it is guaranteed to return an optimal solution. If the heuristic function used by A* is admissible, then A* is admissible.
Consistency: The estimate of heuristic function is always less than or equal to the estimated distance from any neighbouring vertex to the goal, plus the cost of reaching that neighbour.

h(N) \leq c(N, P) + h(P)

where $c(N, P)$ is the cost from $N$ to $P$ . In other words, heuristic “arc” cost less than the actual cost for each arc.

Consistency ensures that the estimated total cost $f(n) = g(n) + h(n)$ is non-decreasing along any path. This means once A* expands a node, the cost found for that node is the lowest possible, and the node will not need to be re-expanded later. It leads to more efficient searches.

For tree search, A* is optimal if heuristic is admissible; for graph search, A* is optimal if heuristic is consistent. In general, most natural admissible heuristics tend to be consistent, especially if from relaxed problems.

Completeness: On finite graphs with non-negative edge weights A* is guaranteed to terminate and is complete, i.e. it will always find a solution (a path from start to goal) if one exists.


99 collapsed lines
1
import java.util.*;
2

3
public class AStarSearch {
4
    public static class Node implements Comparable<Node> {
5
        int x, y;
6
        double f, g, h;
7
        Node parent;
8

9
        public Node(int x, int y) {
10
            this.x = x;
11
            this.y = y;
12
        }
13

14
        @Override
15
        public int compareTo(Node other) {
16
            return Double.compare(this.f, other.f);
17
        }
18

19
        @Override
20
        public boolean equals(Object obj) {
21
            if (this == obj) return true;
22
            if (!(obj instanceof Node other)) return false;
23
            return this.x == other.x && this.y == other.y;
24
        }
25

26
        @Override
27
        public int hashCode() {
28
            return Objects.hash(x, y);
29
        }
30
    }
31

32
    private static boolean isValid(int[][] grid, int x, int y) {
33
        return (x >= 0 && x < grid.length &&
34
                y >= 0 && y < grid[0].length &&
35
                grid[x][y] == 0);
36
    }
37

38
    // Manhattan distance
39
    private static double heuristic(Node a, Node b) {
40
        return Math.abs(a.x - b.x) + Math.abs(a.y - b.y);
41
    }
42

43
    public static List<Node> aStar(int[][] grid, Node start, Node goal) {
44
        PriorityQueue<Node> openSet = new PriorityQueue<>();
45
        Set<Node> closedSet = new HashSet<>();
46

47
        start.g = 0;
48
        start.h = heuristic(start, goal);
49
        start.f = start.g + start.h;
50
        openSet.add(start);
51

52
        while (!openSet.isEmpty()) {
53
            Node current = openSet.poll();
54

55
            if (current.equals(goal)) {
56
                return reconstructPath(current);
57
            }
58

59
            closedSet.add(current);
60

61
            int[][] directions = { {0, 1}, {1, 0}, {0, -1}, {-1, 0} };
62
            for (int[] dir : directions) {
63
                int newX = current.x + dir[0];
64
                int newY = current.y + dir[1];
65
                if (!isValid(grid, newX, newY))
66
                    continue;
67

68
                Node neighbor = new Node(newX, newY);
69
                if (closedSet.contains(neighbor))
70
                    continue;
71

72
                double tentativeG = current.g + 1;
73

74
                boolean inOpenSet = openSet.contains(neighbor);
75
                if (!inOpenSet || tentativeG < neighbor.g) {
76
                    neighbor.parent = current;
77
                    neighbor.g = tentativeG;
78
                    neighbor.h = heuristic(neighbor, goal);
79
                    neighbor.f = neighbor.g + neighbor.h;
80

81
                    if (!inOpenSet) {
82
                        openSet.add(neighbor);
83
                    }
84
                }
85
            }
86
        }
87
        return null;
88
    }
89

90
    private static List<Node> reconstructPath(Node current) {
91
        List<Node> path = new ArrayList<>();
92
        while (current != null) {
93
            path.add(current);
94
            current = current.parent;
95
        }
96
        Collections.reverse(path);
97
        return path;
98
    }
99
}


113 collapsed lines
1
#ifndef ASTARSEARCH_H
2
#define ASTARSEARCH_H
3

4
#include <vector>
5
#include <queue>
6
#include <cmath>
7
#include <algorithm>
8
#include <utility>
9

10
struct Node {
11
    int x, y;
12
    double f, g, h;
13
    Node* parent;
14

15
    Node(const int x, const int y) : x(x), y(y), f(0), g(0), h(0), parent(nullptr) {}
16

17
    bool operator==(const Node& other) const {
18
        return x == other.x && y == other.y;
19
    }
20
};
21

22
struct CompareNode {
23
    bool operator()(const Node* a, const Node* b) const {
24
        return a->f > b->f;
25
    }
26
};
27

28
namespace AStar {
29
    // Manhattan distance heuristic
30
    inline double heuristic(const Node* a, const Node* b) {
31
        return std::abs(a->x - b->x) + std::abs(a->y - b->y);
32
    }
33

34
    // Check if cell (x, y) is valid and walkable in the grid
35
    inline bool isValid(const std::vector<std::vector<int>>& grid, int x, int y) {
36
        return (x >= 0 && x < grid.size() &&
37
                y >= 0 && y < grid[0].size() &&
38
                grid[x][y] == 0);
39
    }
40

41
    // Reconstruct the path from goal to start by following parent pointers.
42
    inline std::vector<std::pair<int, int>> reconstructPath(Node* current) {
43
        std::vector<std::pair<int, int>> path;
44
        while (current != nullptr) {
45
            path.emplace_back(current->x, current->y);
46
            current = current->parent;
47
        }
48
        std::ranges::reverse(path);
49
        return path;
50
    }
51

52
    // A* search algorithm.
53
    // Note: For simplicity, this example does not free allocated memory.
54
    inline std::vector<std::pair<int, int>> aStar(const std::vector<std::vector<int>>& grid, Node* start, const Node* goal) {
55
        std::priority_queue<Node*, std::vector<Node*>, CompareNode> openSet;
56
        std::vector<Node*> closedSet;
57

58
        start->g = 0;
59
        start->h = heuristic(start, goal);
60
        start->f = start->g + start->h;
61
        openSet.push(start);
62

63
        constexpr int directions[4][2] = { {0, 1}, {1, 0}, {0, -1}, {-1, 0} };
64

65
        while (!openSet.empty()) {
66
            Node* current = openSet.top();
67
            openSet.pop();
68

69
            // Goal check
70
            if (*current == *goal) {
71
                return reconstructPath(current);
72
            }
73

74
            closedSet.push_back(current);
75

76
            // Explore neighbors
77
            for (const auto direction : directions) {
78
                const int newX = current->x + direction[0];
79
                const int newY = current->y + direction[1];
80

81
                if (!isValid(grid, newX, newY))
82
                    continue;
83

84
                auto neighbor = new Node(newX, newY);
85

86
                // Skip if neighbor is in closedSet
87
                bool skip = false;
88
                for (const Node* closedNode : closedSet) {
89
                    if (*closedNode == *neighbor) {
90
                        skip = true;
91
                        break;
92
                    }
93
                }
94
                if (skip) {
95
                    delete neighbor;
96
                    continue;
97
                }
98

99
                const double tentativeG = current->g + 1;
100

101
                neighbor->parent = current;
102
                neighbor->g = tentativeG;
103
                neighbor->h = heuristic(neighbor, goal);
104
                neighbor->f = neighbor->g + neighbor->h;
105
                openSet.push(neighbor);
106
            }
107
        }
108

109
        return {};
110
    }
111
}
112

113
#endif // ASTARSEARCH_H


84 collapsed lines
1
import heapq
2

3
class Node:
4
    def __init__(self, x, y):
5
        self.x = x
6
        self.y = y
7
        self.f = 0.0
8
        self.g = 0.0
9
        self.h = 0.0
10
        self.parent = None
11

12
    def __lt__(self, other):
13
        return self.f < other.f
14

15
    def __eq__(self, other):
16
        if other is None:
17
            return False
18
        return self.x == other.x and self.y == other.y
19

20
    def __hash__(self):
21
        return hash((self.x, self.y))
22

23
def is_valid(grid, x, y):
24
    return (0 <= x < len(grid) and
25
            0 <= y < len(grid[0]) and
26
            grid[x][y] == 0)
27

28
def heuristic(a, b):
29
    return abs(a.x - b.x) + abs(a.y - b.y)
30

31
def a_star(grid, start, goal):
32
    open_set = []
33
    closed_set = set()
34

35
    start.g = 0
36
    start.h = heuristic(start, goal)
37
    start.f = start.g + start.h
38
    heapq.heappush(open_set, (start.f, start))
39

40
    while open_set:
41
        current_f, current_node = heapq.heappop(open_set)
42
        if current_node == goal:
43
            return reconstruct_path(current_node)
44

45
        closed_set.add(current_node)
46

47
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
48
        for dir_x, dir_y in directions:
49
            new_x = current_node.x + dir_x
50
            new_y = current_node.y + dir_y
51
            if not is_valid(grid, new_x, new_y):
52
                continue
53

54
            neighbor = Node(new_x, new_y)
55
            if neighbor in closed_set:
56
                continue
57

58
            tentative_g = current_node.g + 1
59

60
            in_open_set = False
61
            for _, node_in_open_set in open_set:
62
                if node_in_open_set == neighbor:
63
                    in_open_set = True
64
                    break
65

66
            if not in_open_set or tentative_g < neighbor.g:
67
                neighbor.parent = current_node
68
                neighbor.g = tentative_g
69
                neighbor.h = heuristic(neighbor, goal)
70
                neighbor.f = neighbor.g + neighbor.h
71

72
                if not in_open_set:
73
                    heapq.heappush(open_set, (neighbor.f, neighbor))
74
                else:
75
                    pass
76

77
    return None
78

79
def reconstruct_path(current_node):
80
    path = []
81
    while current_node:
82
        path.append(current_node)
83
        current_node = current_node.parent
84
    return path[::-1]

1.3 Constraint Satisfaction Problems (CSPs)

Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. In CSPs, state is defined by variables $X_i$ with values froma domain $D_i$ , and the goal test is a set of constraints specifying allowable combinations of values for subsets of variables.

For example, for the map coloring problem below,

\text{variables} = \{WA, NT, Q, NT, NSW, V, SA, T\}

\text{domains} = \{ \text{red}, \text{green}, \text{blue} \}

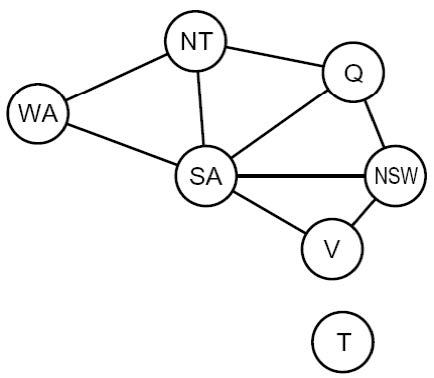
1.3.1 Varieties of CSPs and Constraints

Varieties of CSPs

Discrete Variables:
- Finite domains: e.g., map coloring.
- Infinite domains: e.g., job scheduling, variables are start/end times for each job.
Continuous Variables: e.g., start/end times for Hubble Telescope observations.

Varieties of Constraints

Unary constraints involve a single variable (e.g., $X_1 \neq 1$ ).
Binary constraints involve pairs of variables (e.g., $X_1 \neq X_2$ ).
Higher-order constraints involve three or more variables (e.g., cryptarithmetic column constraints).

1.3.2 Backtracking Search

Backtracking is a class of algorithms that incrementally builds candidates to the solutions, and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot possibly be completed to a valid solution. This is based on the idea of depth-first search, with two more improvements:

Pruning (Check constraints as you go): If a partial assignment violates a constraint, we can prune the search space by not considering any extensions of that assignment. E.g., if $X_1 = 1$ and $X_1 \neq X_2$ , we can prune any assignment of $X_2$ that is equal to 1.
Filtering (Forward checking): If a variable is assigned, we can remove any inconsistent values from the domains of the remaining unassigned variables. E.g., if $X_1 = 1$ and $X_1 \neq X_2$ , we can directly remove 1 from the domain of $X_2$ when we assign $X_1$ instead of waiting until we assign $X_2$ .