Part Ⅱ
9 Symbol Table & Binary Search Tree
9.1 Symbol Table & Elementary Implementation
Symbol table: Key-value pair abstraction.
Insert a value with a specified key.
Given a key, search for the corresponding value.
9.1.1 Unordered List Implementation
Method: Maintain an (unordered) linked list of key-value pairs.
Search: Scan through all keys until find a match (sequential search).
Insert: Scan through all keys until find a match; if no match add to front.
9.1.2 Ordered Array Implementation
Method: Maintain an ordered array of key-value pairs.
Search: Binary search
Insert: Need to shift all greater keys over.
9.2 Ordered Operation
Provide an interface that can give clients ordered symbol tables!
9.3 Binary Search Trees
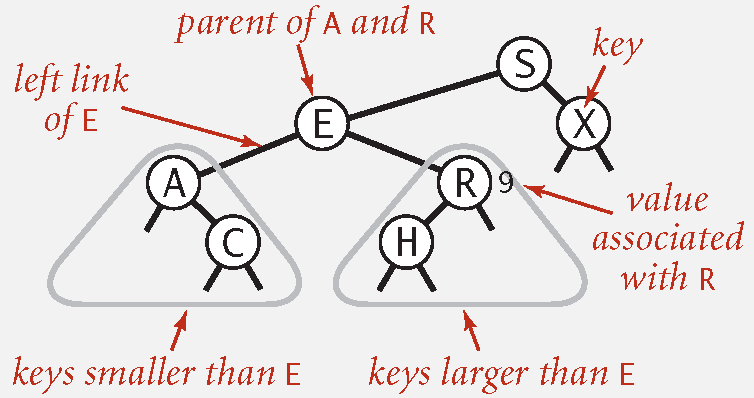
Binary Saerch Tree: A BST is a binary tree in symmetric order.
A binary tree is either:
Empty.
Two disjoint binary trees (left and right).
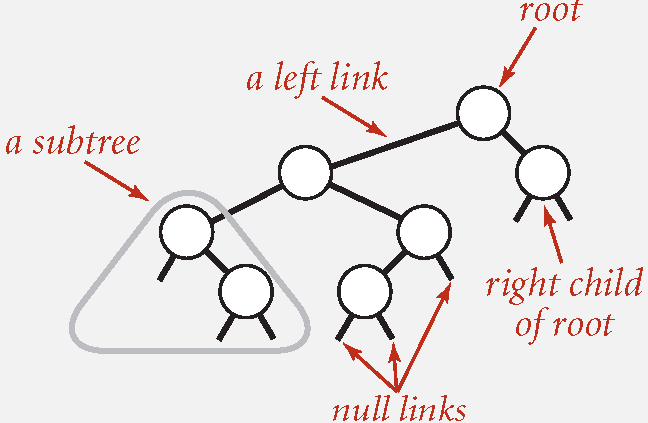
Symmetric order: Each node has a key, and every node's key is:
Larger than all keys in the left subtree.
Smaller than all keys in the right subtree.
BST Search
If less, go left.
If greater, go right.
If equal, search hit.
BST Insertion
Search for keys, then two cases:
Key in tree => reset value
Key not in tree => add new node
Property: If
Proof: 1-1 correspondence with quicksort partitioning.
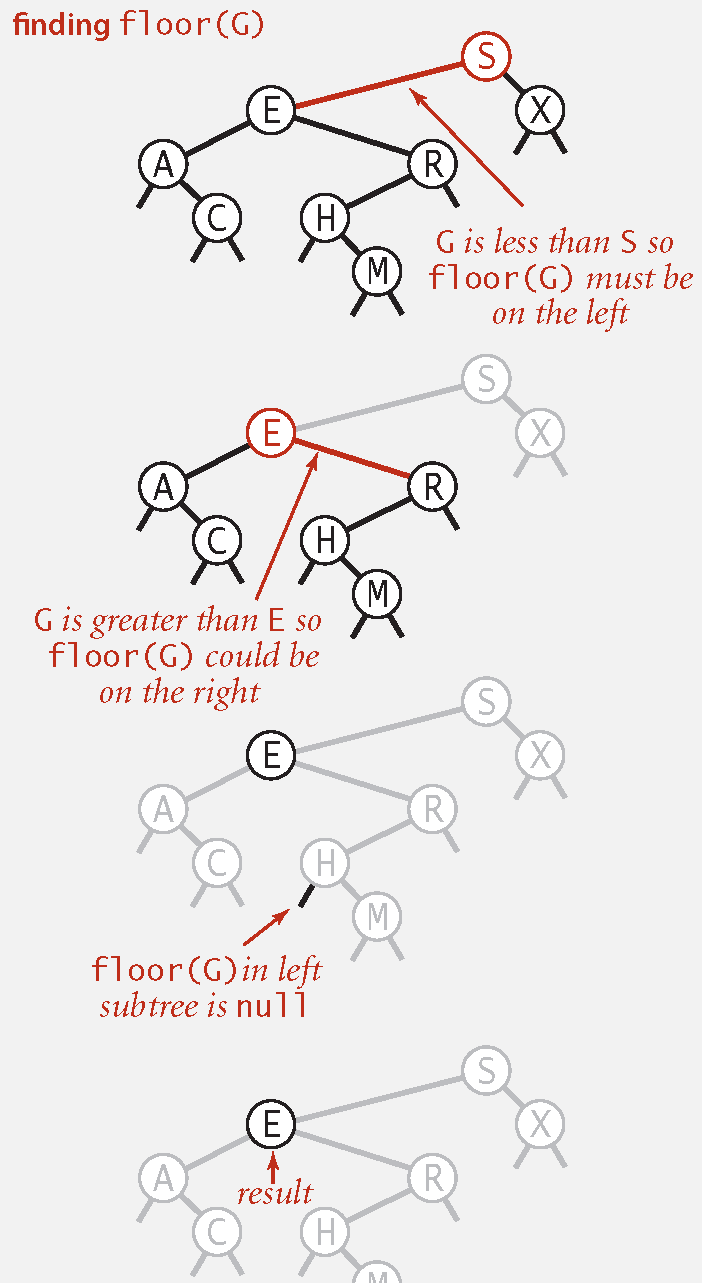
Floor: Largest key <= to a given key.
Ceiling: Smallest key >= to a given key.
Rank: How many keys < k
Computing the Floor
equals to the key at the root. => The floor of is . is less than the key at the root. => The floor of is in the left subtree. is greater than the key at the root. => The floor of is in the right subtree (if there is any key ); otherwise, it is the key at the root.
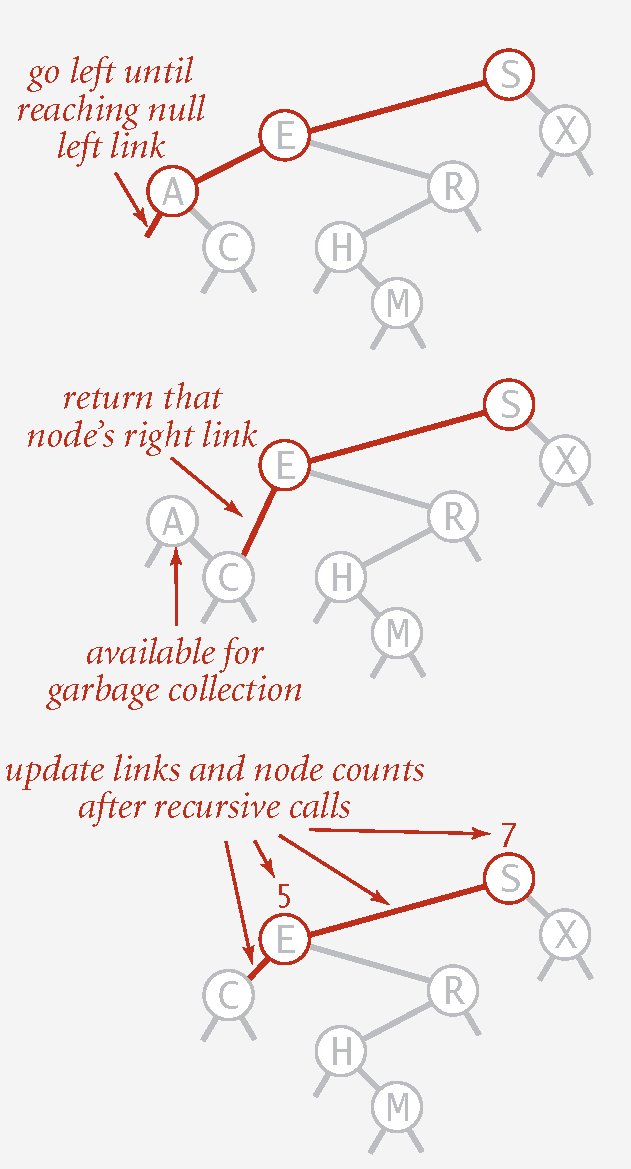
Deleting the Minimum
Go left until finding a node with a null left link.
Replace that node by its right link.
Update subtree counts.
Habbard Deletion
0 children: Delete
by setting parent link to null. 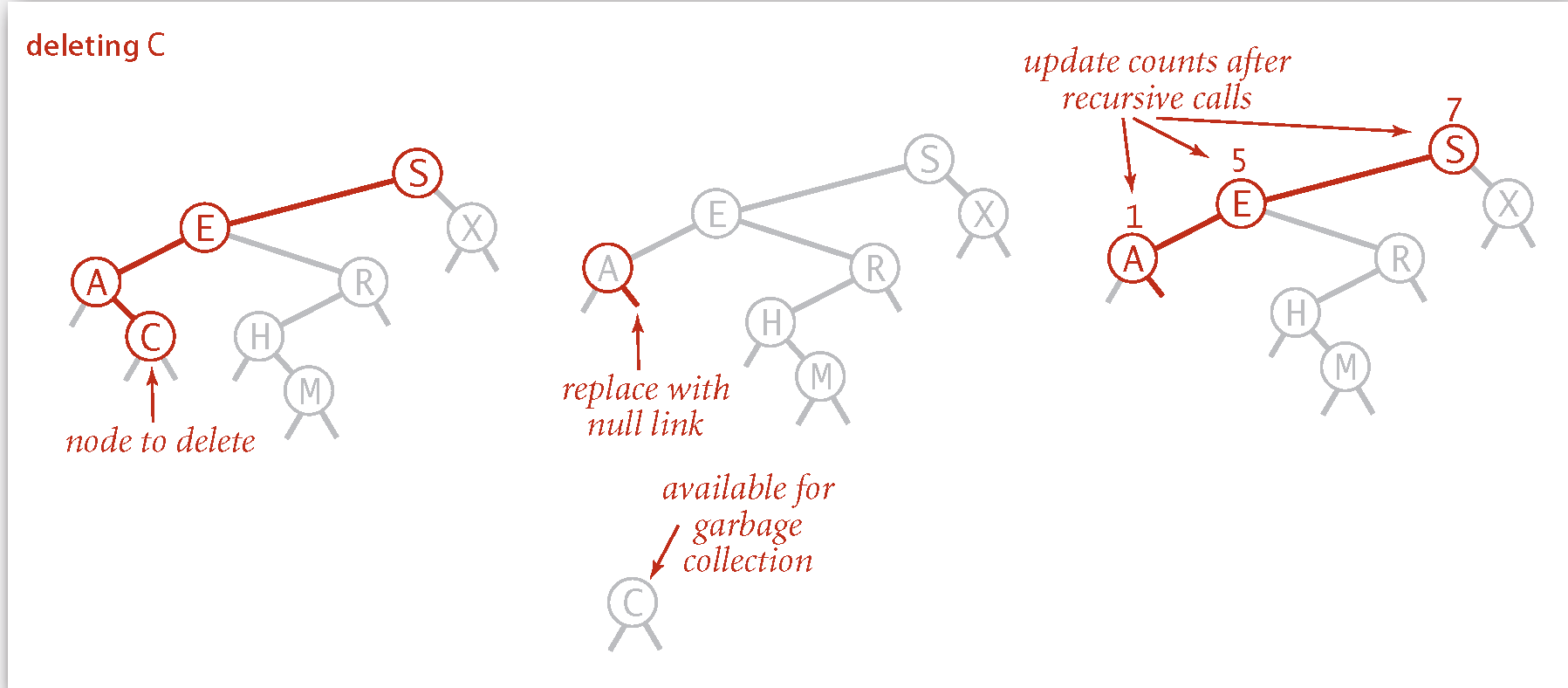
1 child: Delete
by replacing parent link. 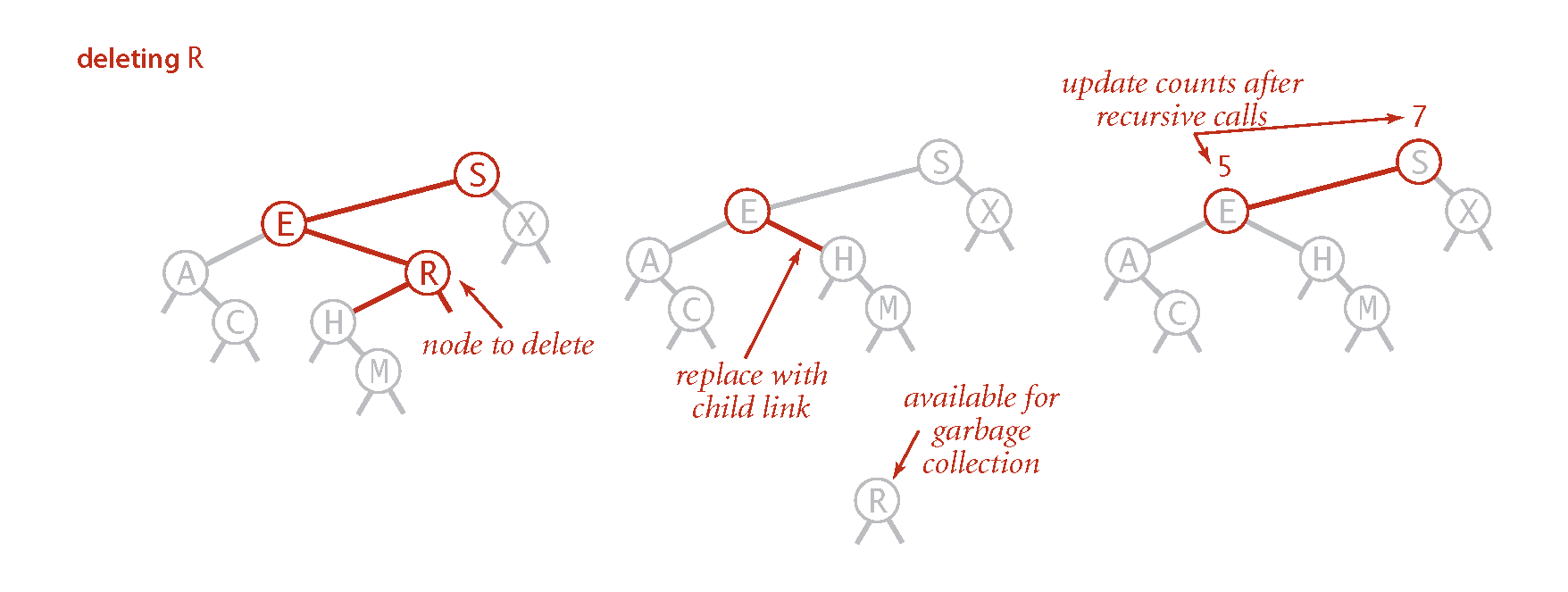
2 children:
Find successor
of . Delete the minimum in its
's right subtree . Put
in 's spot.
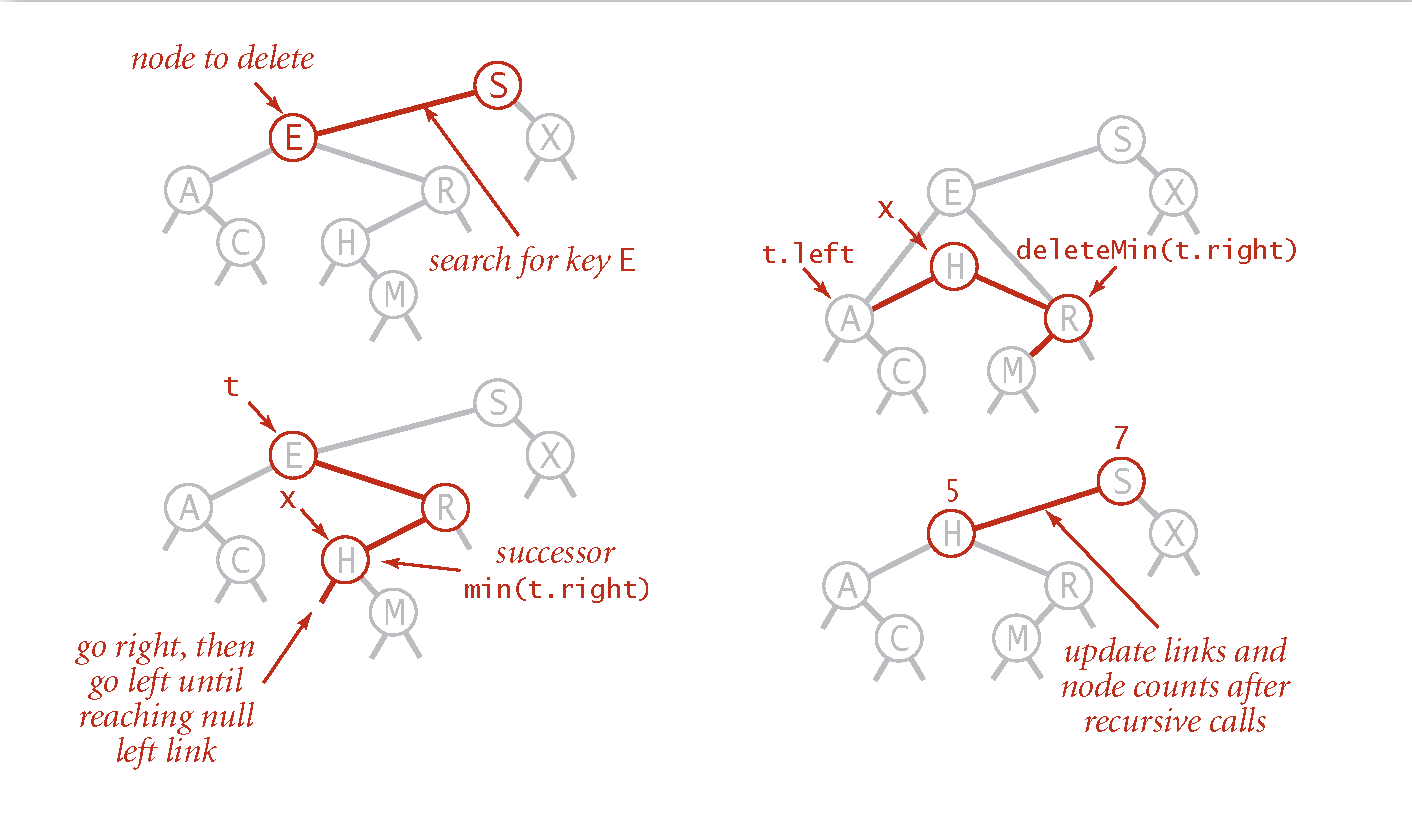
9.4 Traversal
To traverse binary trees with depth-first search, execute the following three operations in a certain order:
N: Visit the current node.
L: Recursively traverse the current node's left subtree.
R: Recursively traverse the current node's right subtree.
Three types of traversal
Pre-order => NLR
Post-order => LRN
In-order => LNR
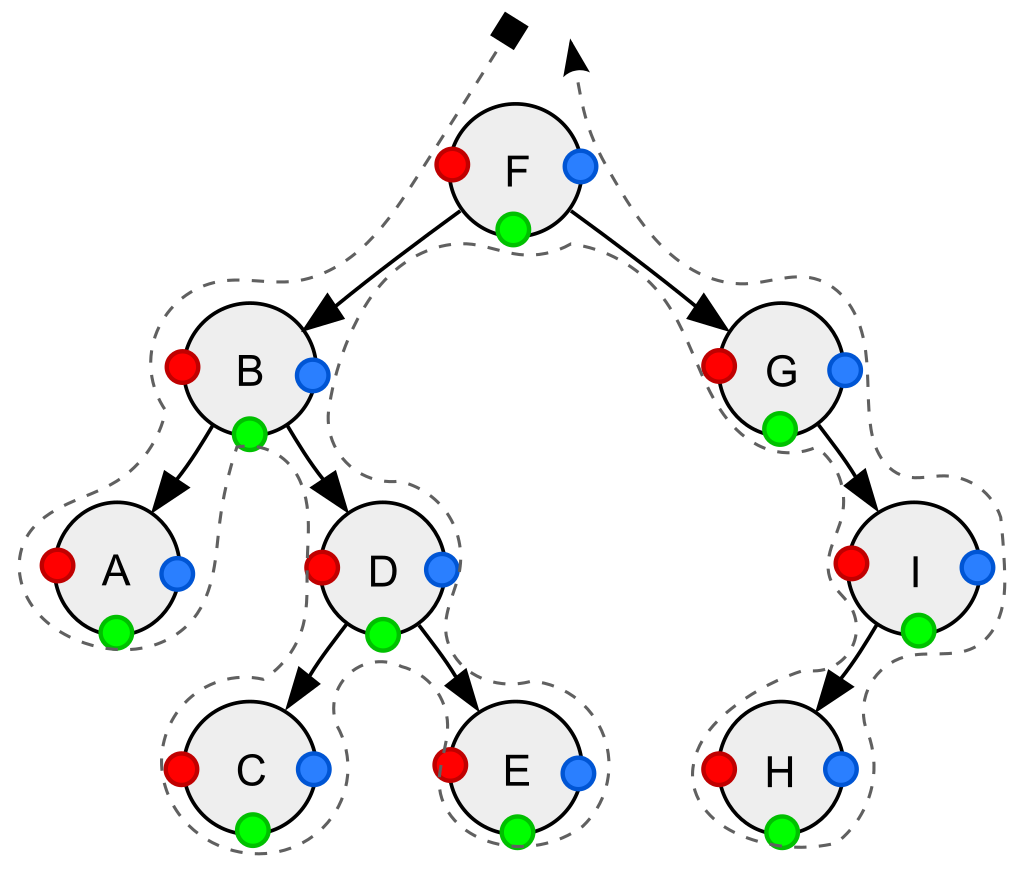
Depth-first traversal (dotted path) of a binary tree:
Pre-order (node visited at position red):
F, B, A, D, C, E, G, I, H;
In-order (node visited at position green):
A, B, C, D, E, F, G, H, I;
Post-order (node visited at position blue):
A, C, E, D, B, H, I, G, F.
Level Order (breadth-first traversal) : Visit all the nodes of a tree data structure level by level.
Level Order Traversal
Start at the root node.
Visit all the nodes at the current level.
Move to the next level, repeat steps 2 and 3 until all levels of the tree have been visited.
10 Balanced Search Trees
Implementation | Worst-Case Cost (after | Average Case (after | Ordered Iteration? | Key Interface | ||||
Search | Insert | Delete | Search Hit | Insert | Delete | |||
no |
| |||||||
yes |
| |||||||
? | yes |
| ||||||
yes |
| |||||||
yes |
| |||||||
10.1 2-3 Trees
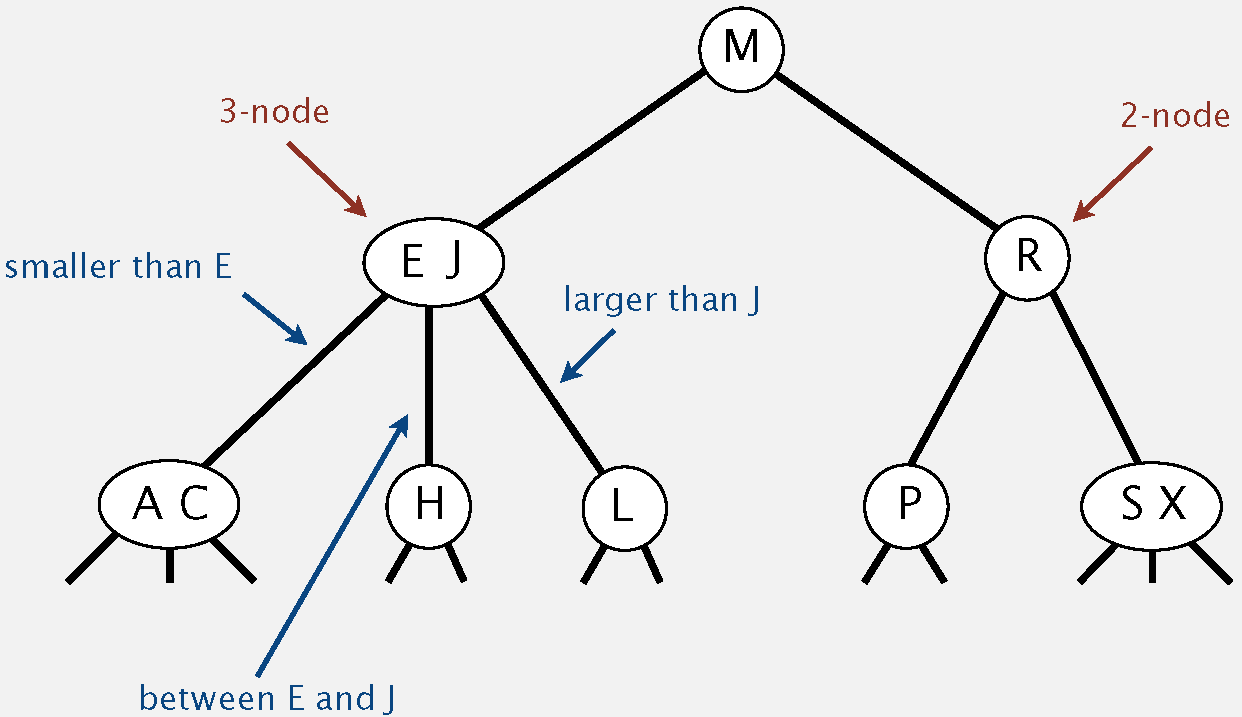
2-3 Tree
Allow 1 or 2 keys per node.
2-node: one key, two children.
3-node: two keys, three children.
Searching in 2-3 Tree
Compare search key against keys in node.
Find interval containing search key.
Follow associated key (recursively).
Inserting into a 2-node At Bottom
Search for key, as usual.
Replace 2-node with 3-node.
Inserting into a 3-node At Bottom
Add new key to 3-node to create a temporary 4-node.
Move middle key in 4-node into a parent.
Repeat up the tree, as necessary.
If you reach the root and it's a 4-node, split it into three 2-nodes.
Properties
Maintain symmetric order and perfect balance: Every path from root to null link has same length.
Proof
Worst case:
=> all 2-nodes Best case:
=> all 3-nodes Between 12 and 20 for a million nodes.
Between 18 and 30 for a billion nodes.
Guaranteed logarithmic performance for search and insert.
10.2 Red-Black BSTs
10.2.1 Left-Leaning Red-Black BSTs
Definition 1:
Represent 2–3 tree as a BST.
Use "internal" left-leaning links as "glue" for 3–nodes.
Definition 2: A BST such that:
No node has two red links connected to it.
Every path from root to null link has the same number of black links.
Red links lean left.

10.2.2 Elementary Red-Black BST Operations
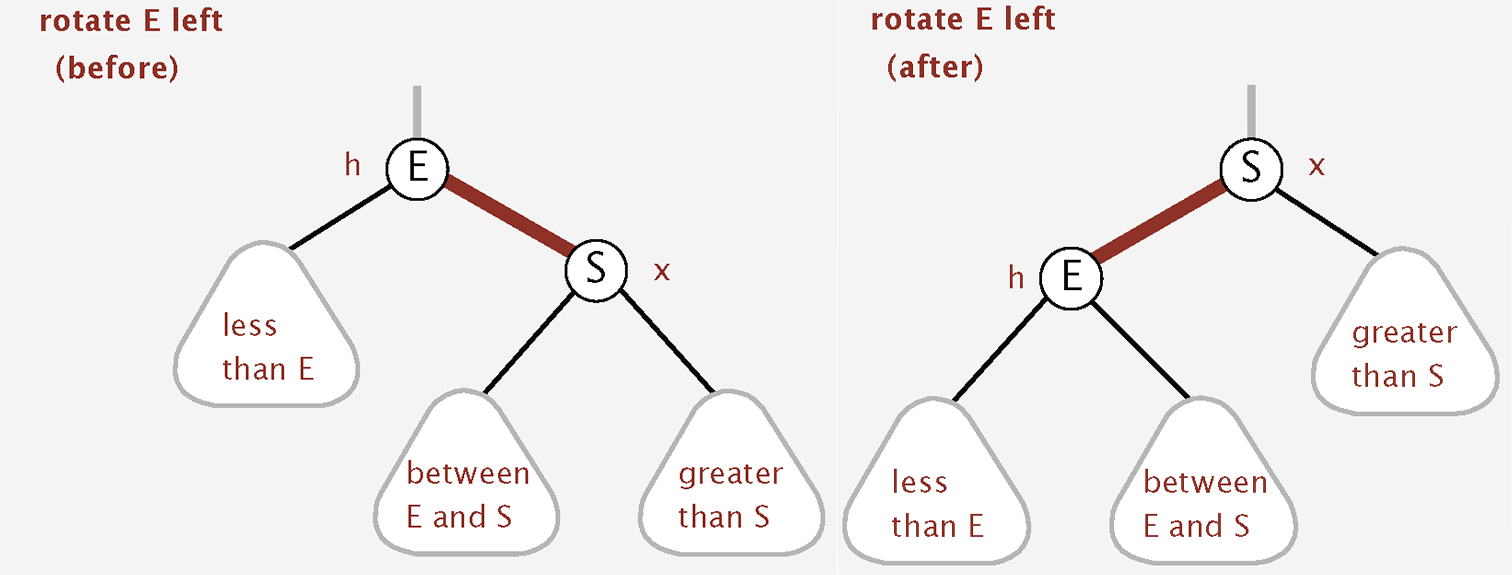
Left rotation: Orient a (temporarily) right-leaning red link to lean left.
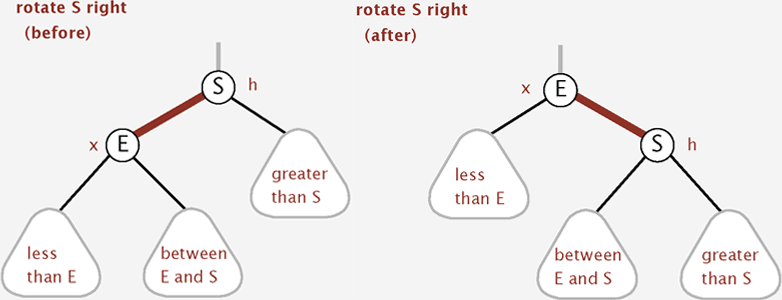
Right rotation: Orient a left-leaning red link to (temporarily) lean right.
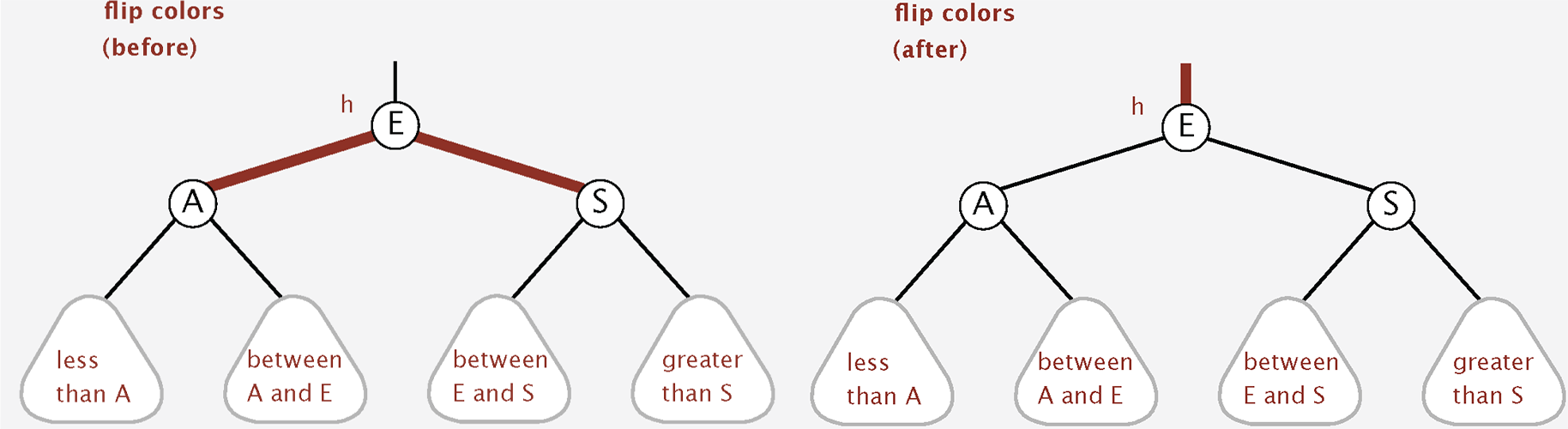
Color flip: Recolor to split a (temporary) 4-node.
10.2.3 Red-Black BST Operations
Case 1: Insert into a 2-node at the bottom | Insert into a tree with exactly 1 node
Do standard BST insert; color new link red.
If new red link is a right link, rotate left.
Case 2: Insert into a 3-node at the bottom | Insert into a tree with exactly 2 nodes.
Do standard BST insert; color new link red.
Rotate to balance the 4-node (if needed).
Flip colors to pass red link up one level.
Rotate to make lean left (if needed).
Repeat case 1 or case 2 up the tree (if needed).
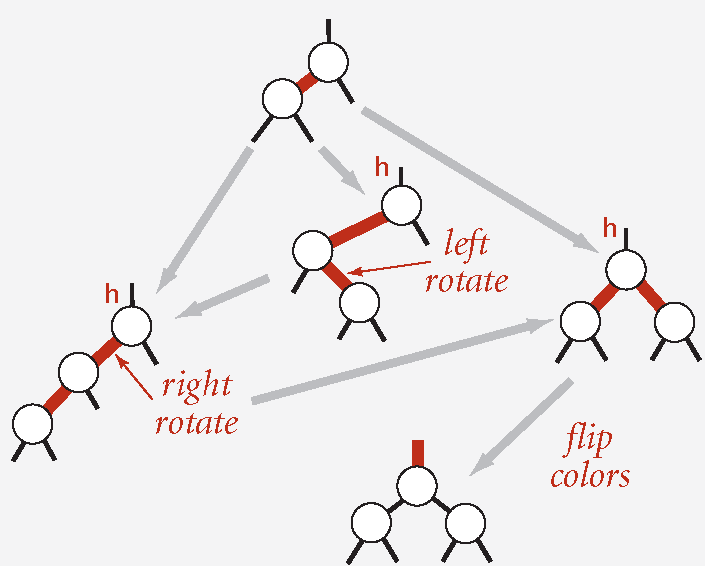
Insertion for Red-Black BSTs
Right child red, left child black: rotate left.
Left child, left-left grandchild red: rotate right.
Both children red: flip colors.
10.2.4 Red-Black BST Implementations
10.2.5 Red-Black BST Properties and Applications
Properties
Height of tree is
in the worst case. Proof: Every path from root to null link has same of black links. Never two red links in-a-row .
Height of tree is
in typical applications.
Applications: Red-black trees are widely used as system symbol tables.
Java:
java.util.TreeMap,java.util.TreeSetC++ STL: map, multimap, multiset
Linux kernel: completely fair scheduler, linux/rbtree.h
Emacs: conservative stack scanning
10.3 B-Trees
Background Information:
Page: Continuous block of data (e.g., a file or 4,096-byte chunk).
Probe: First access to a page (e.g., from disk to memory).
Property: Time required for a probe is much higher than time to access data within a page.
Goal: Access data using minimum number of probes.
Definition:
B-tree (Bayer-McCreight, 1972): Generalize 2-3 trees by allowing up to
key-link pairs per node. At least 2 key-link pairs at root.
At least
key-link pairs in other nodes. External nodes contain client keys.
Internal nodes contain copies of keys to guide search.
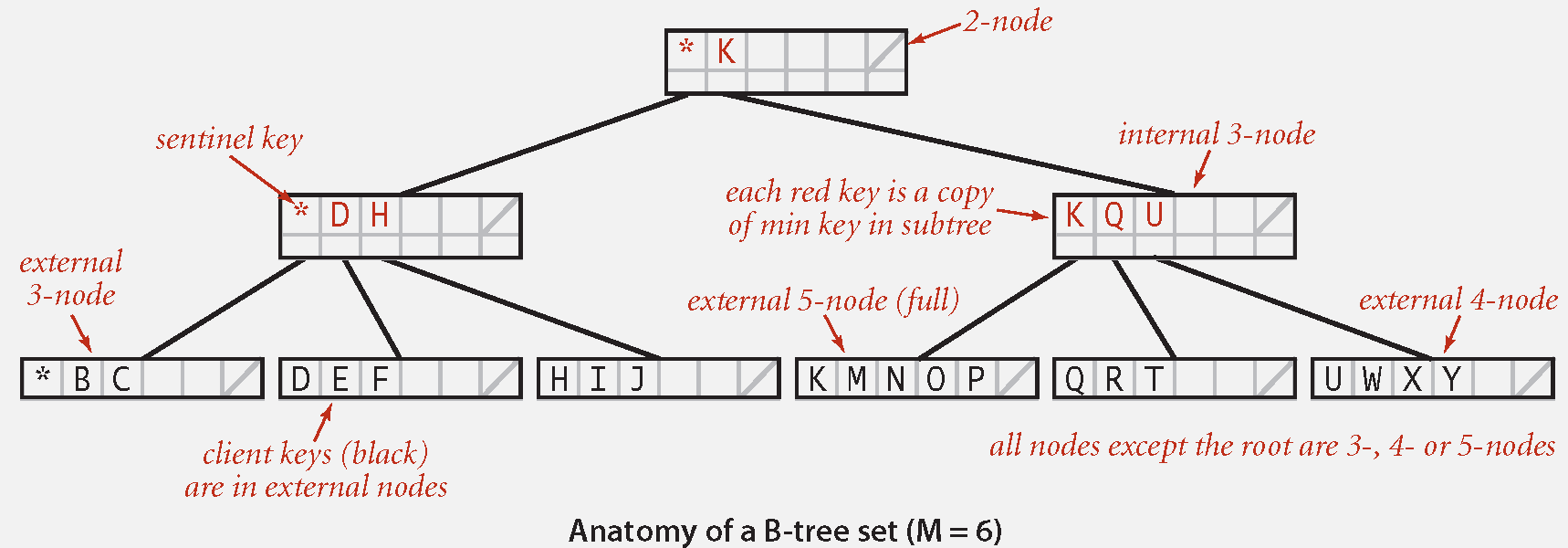
Property:
A search or an insertion in a B-tree of order
with keys requires between and probes. Proof: All internal nodes (besides root) have between
and links. In practice: Number of probes is at most 4.
Optimization: Always keep page root in memory.
Applications:
B-trees (and variants B+ Tree, B * Tree, B# Tree) are widely used for file systems and databases.
Windows: NTFS.
Mac: HFS, HFS+.
Linux: ReiserFS, XFS, Ext3FS, JFS.
Databases: ORACLE, DB2, INGRES, SQL, PostgreSQL.
Search in B-Tree
Start at root.
Find interval containing search key.
Follow associated link (recursively).
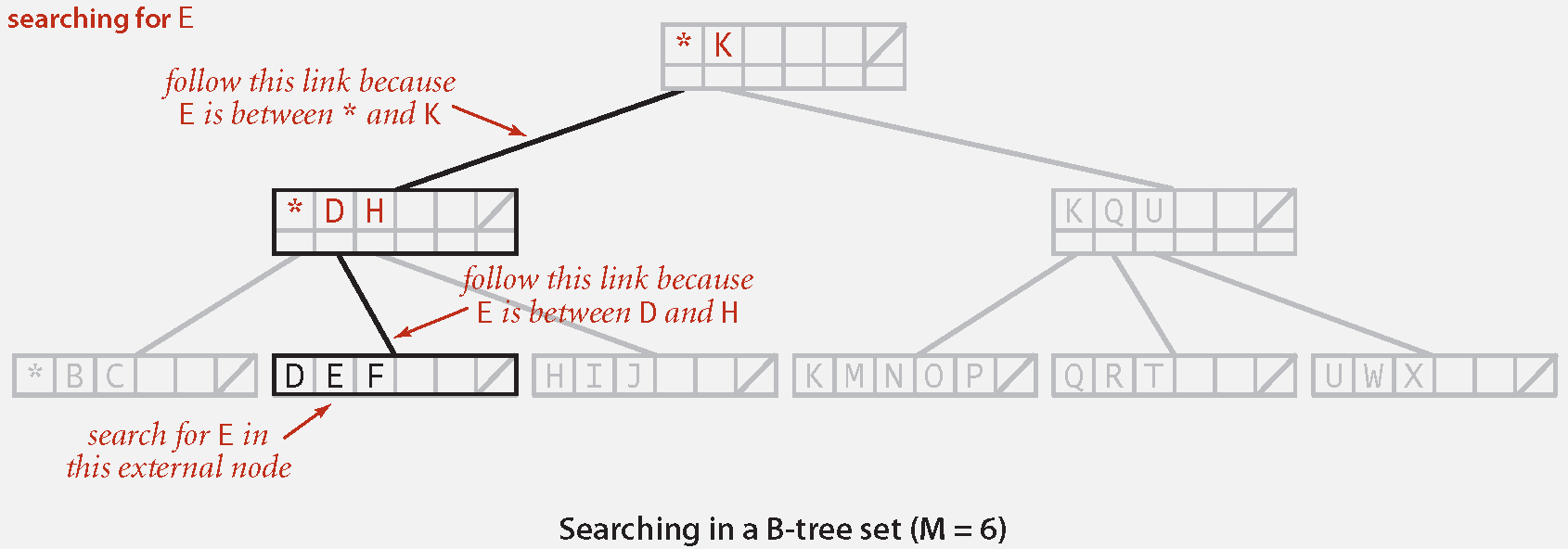
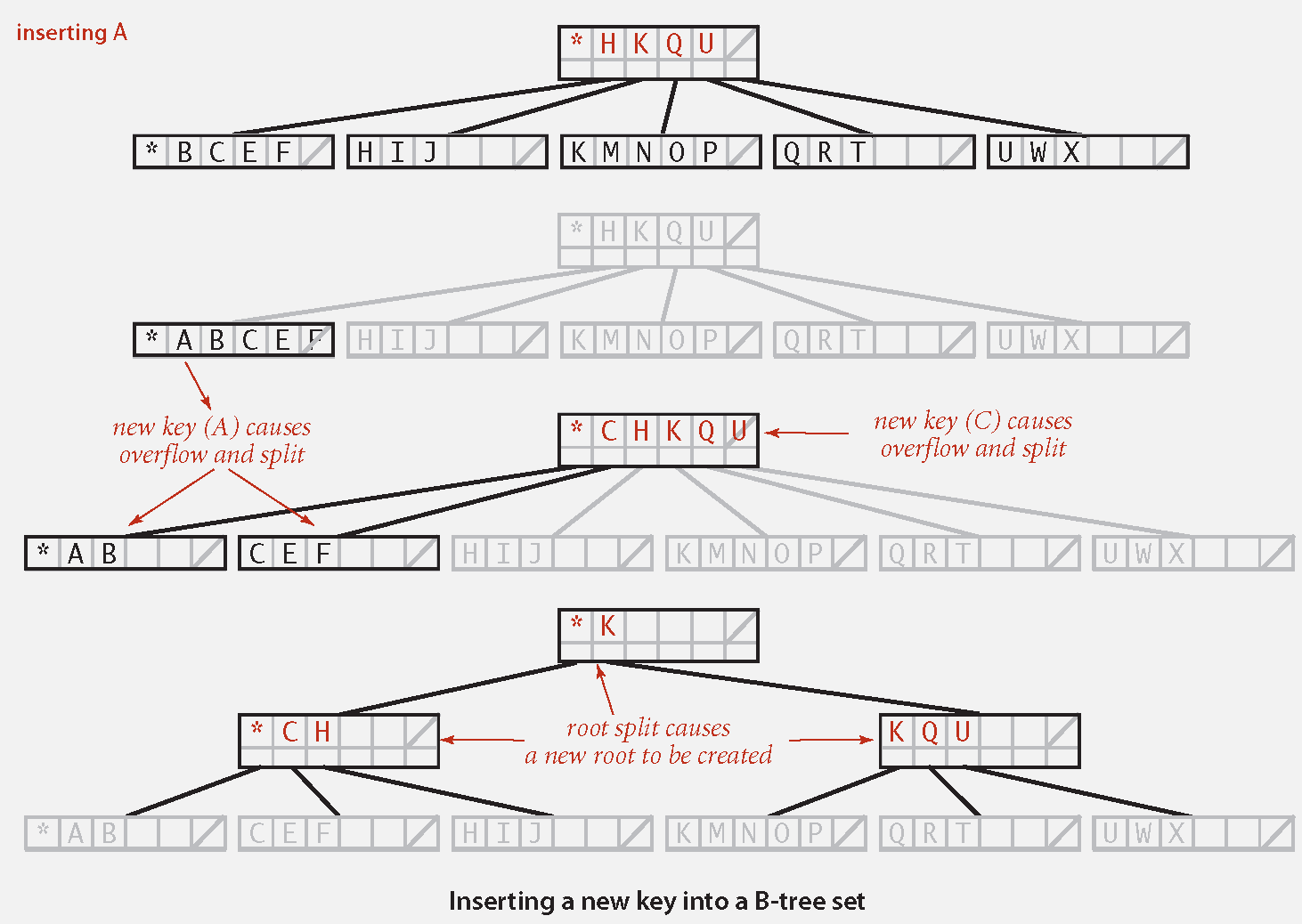
Insert in B-Tree
Search for new key.
Insert at bottom.
Split nodes with
key-link pairs on the way up the tree.
10.4 AVL Trees
AVL trees maintain height-balance (also called the AVL Property).
Skew of a node: The height of of its right subtree minus that of its left subtree.
A node is height-blanced if
. Property: A binary tree with height-balanced nodes has height
. Proof
Suppose adding or removing leaf from a height-balanced tree results in imbalance, skews still have magnitude
Case 1: skew of F is 0 or Case 2: skew of F is 1
=> Perform a left rotation on B.
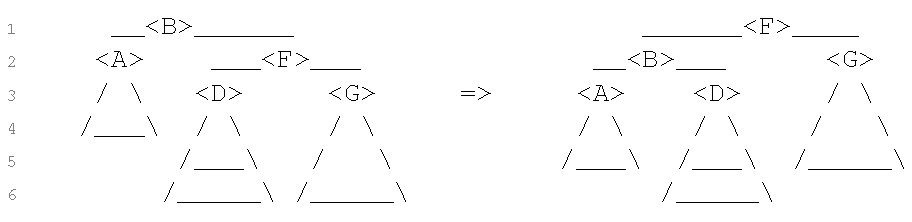
Case 3: skew of F is −1
Perform a right rotation on F, then a left rotation on B
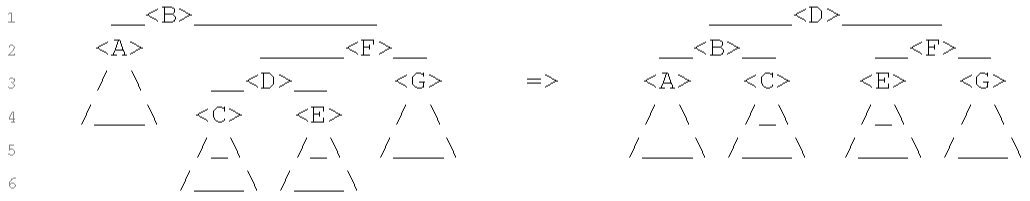
11 Geometric Applications of BSTs
Topic: Intersections among geometric objects.
Applications: CAD, games, movies, virtual reality, databases...
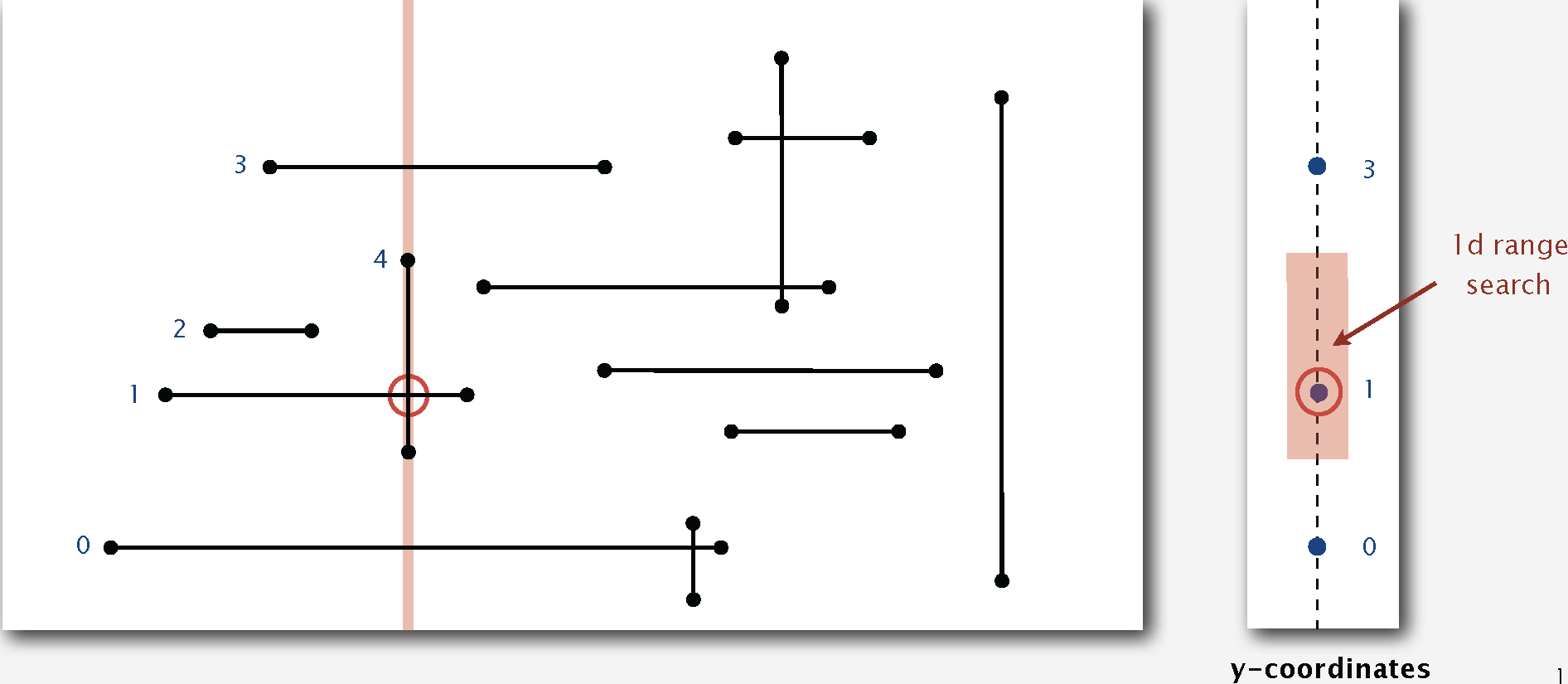
11.1 1d Range Search
Range search: find all key between
Range count:# of keys between
Geometric interpretation: Keys are point on a line; find/count points in a given 1d interval.
1d range count
Recursively find all keys in left subtree (if any could fall in range).
Check key in current node.
Recursively find all keys in right subtree (if any could fall in range).
Property: Running time proportinal to
11.2 Line Segment Intersection
Goal: Given
Sweep-Line Algorithm => Sweep Vertical Lines from Left to Right
Properties: The sweep-line algorithm takes time proportional to
Proof:
Put
Insert
Delete
Range searches in BST. =>
11.3 Kd-Trees
Goal: 2d orthogonal range search.
Geometric interpretation: Keys are point in the plane; find/count points in a given
11.3.1 Grid Implementation
Grid Implementation
Divide space into
Create list of points contained in each square.
Use 2d array to directly index relevant square.
Insert: add
Range search: examine only squares that intersect 2d range query.
Properties:
Space:
Time:
Problems:
Clustering: a well-known phenomenon in geometric data.
Lists are too long, even though average length is short.
Need data structure that adapts gracefully to data.
11.3.2 Space-Partitioning Trees
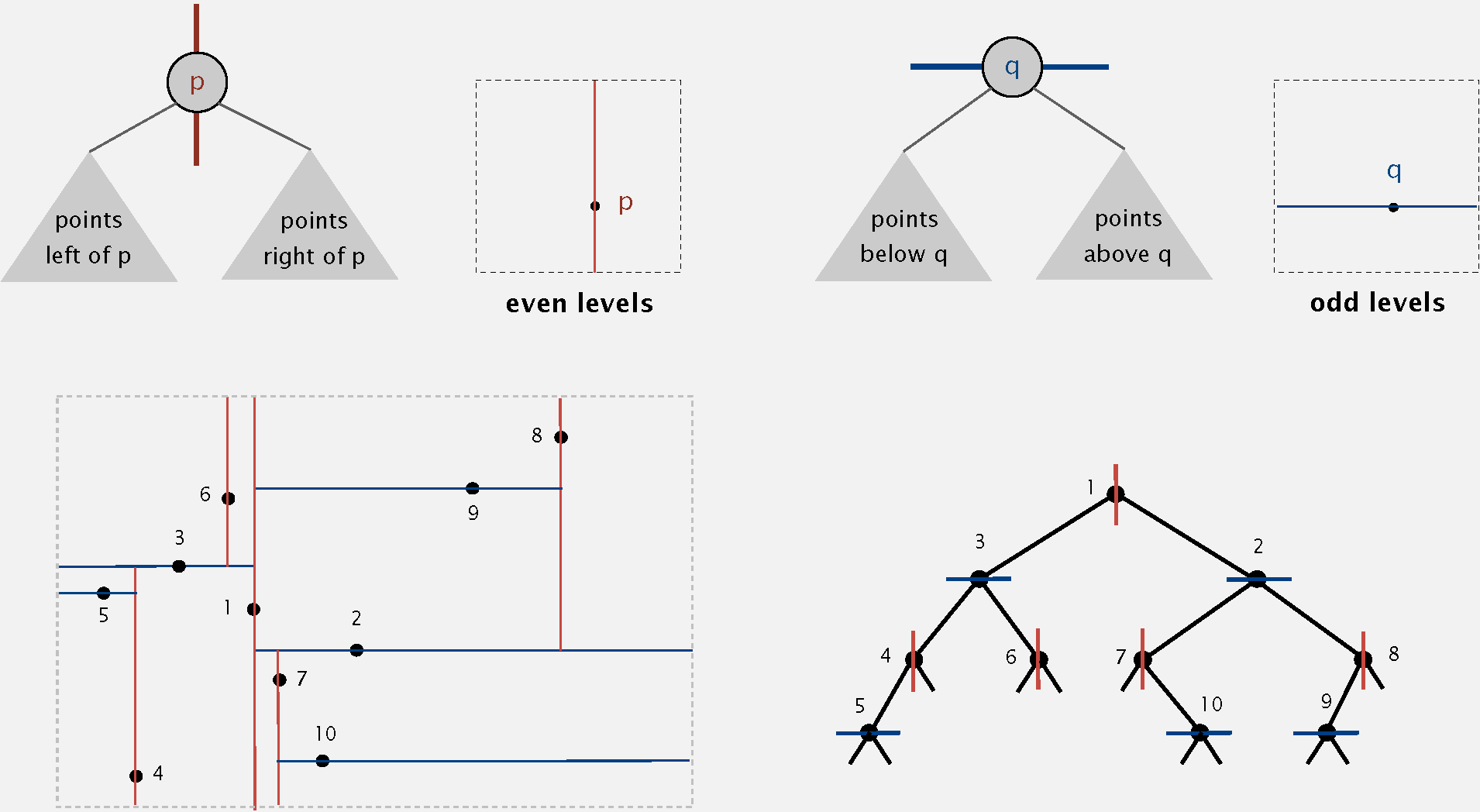
Space-Partitioning Trees: Use a tree to represent a recursive subdivision of a 2d space.
2d Trees: Recursively divide space into two halfplanes.
Applications: Ray tracing, 2d range search, Flight simulators, N-body simulation, Nearest neighbor search, Accelerate rendering in Doom, etc.
Part 1 2d Trees
Data Structure: BST, but alternate using
Search gives rectangle containing point.
Insert further subdivides the plane.
Range Search - Find all points in a query axis-aligned rectangle
Check if point in node lies in given rectangle.
Recursively search left/bottom (if any could fall in rectangle).
Recursively search right/top (if any could fall in rectangle).
Properties
Typical case:
Worst case (assuming tree is balanced):
Nearest Neighbor Search - Find closest point to query point
Check distance from point in node to query point.
Recursively search left/bottom (if it could contain a closer point).
Recursively search right/top (if it could contain a closer point).
Organize method so that it begins by searching for query point.
Properties:
Typical case:
Worst case (even if tree is balanced):
Part 2 Kd Trees
Kd Tree: Recursively partition
Implementation: BST, but cycle through dimensions ala 2d trees.
Part 3 N-body Simulation
Goal: Simulate the motion of
Appel's Algorithm for N-body Simulation
Build 3d-tree with
Store center-of-mass of subtree in each node.
To compute total force acting on a particle, traverse tree, but stop as soon as distance from particle to subdivision is sufficiently large.
Properties: Running time per step is
11.4 Interval Search Tree
Create BST, where each node stores an interval
Use left endpoint as BST key.
Store max endpoint in subtree rooted at node.
Insertion for Interval Search Tree
Insert into BST, using
Update max in each node on search path.
Interval Search for Interval Search Tree
If interval in node intersects query interval, return it.
Else if left subtree is null, go right.
Else if max endpoint in left subtree is less than lo, go right.
Else go left.
Order of growth of running time for
Operation | Brute | Interval search tree | Best in theory |
|---|---|---|---|
Insert interval | |||
Find interval | |||
Delete interval | |||
Find any one interval that intersects | |||
find all interval that intersects |
11.5 Rectangle Intersection
Sweep-line Algorithm
Maintain set of rectangles that intersect the sweep line in an interval search tree (using
Left endpoint: interval search for
Right endpoint: remove
Property: Sweep line algorithm takes time proportional to
Proof
Put
Insert
Delete
Interval searches for y-intervals =>
12 Hash Tables
Implementation | Worst-Case Cost (after | Average Case (after | Ordered Iteration? | Key Interface | ||||
Search | Insert | Delete | Search Hit | Insert | Delete | |||
no |
| |||||||
yes |
| |||||||
? | yes |
| ||||||
yes |
| |||||||
yes |
| |||||||
no |
| |||||||
no |
| |||||||
12.1 Hash Tables
Definitions
Hashing: Save items in a key-indexed table (index is a function of the key).
Hash function: Method for computing array index from key.
Issues:
Equality test: Method for checking whether two keys are equal.
Collision resolution: Algorithm and data structure to handle two keys that hash to the same array index.
Hash code: An int between
Hash function: An int between
12.2 Collision Solution Ⅰ - Separate Chaining & Variant
12.2.1 Separate Chaining
Hash: map key to integer
Insert: put at front of
Search: need to search only
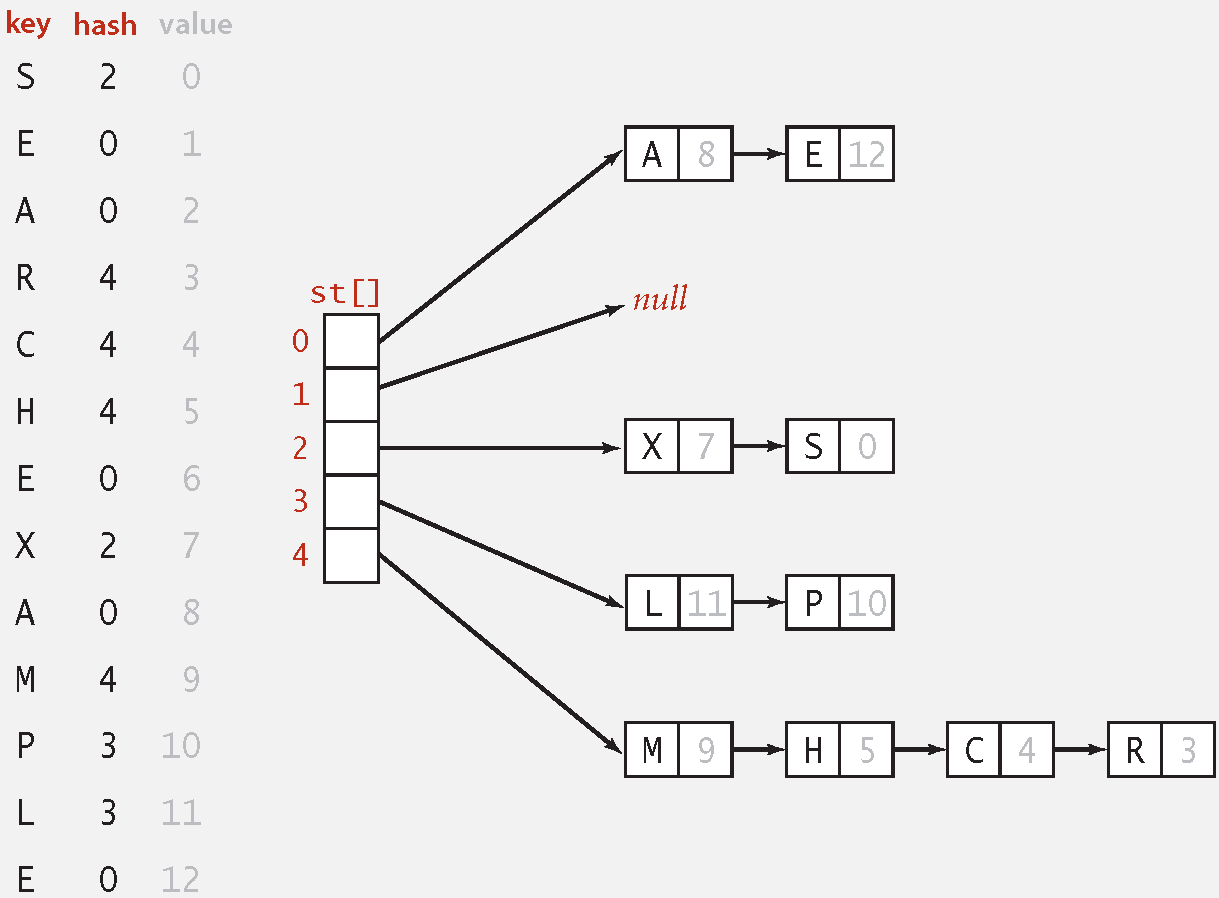
Properties
Number of probes for search/insert/delete is proportional to
Typical choice:
12.2.2 Variant - Two-Probe Hashing
Hash to two positions, insert key in shorter of the two chains.
Reduces expected length of the longest chain to
12.3 Collision Solution Ⅱ - Open Addressing
12.3.1 Linear Probing
Open addressing: When a new key collides, find next empty slot, and put it there.
Hash: Map key to integer
Search: Search table index
Insert: Put at table index
Under uniform hashing assumption, the average numbers of probes in a linear probing hash table of size
Search hit:
Search miss / insert:
Knuth's Parking Problem
Cars arrive at a one-way street with
Half-full: With
Full: With
12.3.2 Varaint 1 - Double Hashing
Use linear probing, but skip a variable amount, not just 1 each time.
Effectively eliminates clustering.
Can allow table to become nearly full.
More difficult to implement delete.
Insert: Use the
12.3.3 Variant 2 - Quadratic Probing
Insert: Use the hash function to calculate index. If there is a collision, probe the index using the following probing sequence:
index 1:
index 2:
index 3:
12.3.4 Variant 3 - Cuckoo Hashing
Hash key to two positions; insert key into either position; if occupied, reinsert displaced key into its alternative position (and recur).
Constant worst case time for search.
12.3.5 Separate Chaining vs. Linear Probing
Separate Chaining
Easier to implement delete.
Performance degrades gracefully.
Clustering less sensitive to poorly-designed hash function.
Linear Probing
Less wasted space.
Better cache performance.
12.4 Hash Table vs. Balanced Search Tree
Hash Table
Simpler to code.
No effective alternative for unordered keys.
Faster for simple keys (a few arithmetic ops versus
Better system support in Java for strings (e.g., cached hash code).
Balanced Search Tree
Stronger performance guarantee.
Support for ordered ST operations.
Easier to implement
compareTo()correctly thanequals()andhashCode().
Java systems includes both.
Red-black BSTs:
java.util.TreeMap,java.util.TreeSet.Hash tables:
java.util.HashMap,java.util.IdentityHashMap.
C++ STL includes both.
Red-black BSTs:
std::set,std::map.Hash tables:
std::unordered_map,std::unordered_set.
13 Symbol Table Applications
13.1 Sets
Mathematical Set: A collection of distinct keys.
13.1.1 Sets in Java
HashSetImplementation: Uses a hash table (specifically, a
HashMapinternally) for storage.Features
Efficient for adding, removing, and checking for the existence of elements (average
Does not maintain insertion order.
Allows a single null element.
LinkedHashSetImplementation: Extends
HashSetand maintains a doubly linked list to preserve the order of element insertion.Features
Elements are iterated in the order they were added.
Slightly slower than
HashSetdue to the linked list overhead.
TreeSetImplementation: Uses a red-black tree (a self-balancing binary search tree).
Features:
Elements are stored in sorted order (natural order or using a
Comparatorprovided during set creation).Provides efficient retrieval of elements in a sorted range.
Slower than
HashSetandLinkedHashSetfor insertion and removal operations (logarithmic time complexity).Does not allow
nullelements by default.
13.1.2 Sets in C++
std::set|std::multisetImplementation: Usually implemented as a self-balancing binary search tree (often a red-black tree).
Features
Elements are stored in sorted order (by default, using
std::less, which is the less-than operator <)Most operations like insertion, search, deletion, etc., have a time complexity of
std::unordered_set|std::unordered_multisetImplementation Using a hash table, which prioritizes fast average-case performance for operations like insertion, search, and deletion over maintaining a specific order.
Features
Offers O(1) average-case time complexity for insertion, search, and deletion operations.
13.1.3 Sets in Python
For more information, please visit Sets in Python Programming
13.2 Dictionary Clients
For more information about dictionaries in Python, please visit Python Programming.
13.3 Indexing Clients
13.4 Sparse Vectors
14 Undirected Graphs
14.1 Introduction to Graphs
Terminology
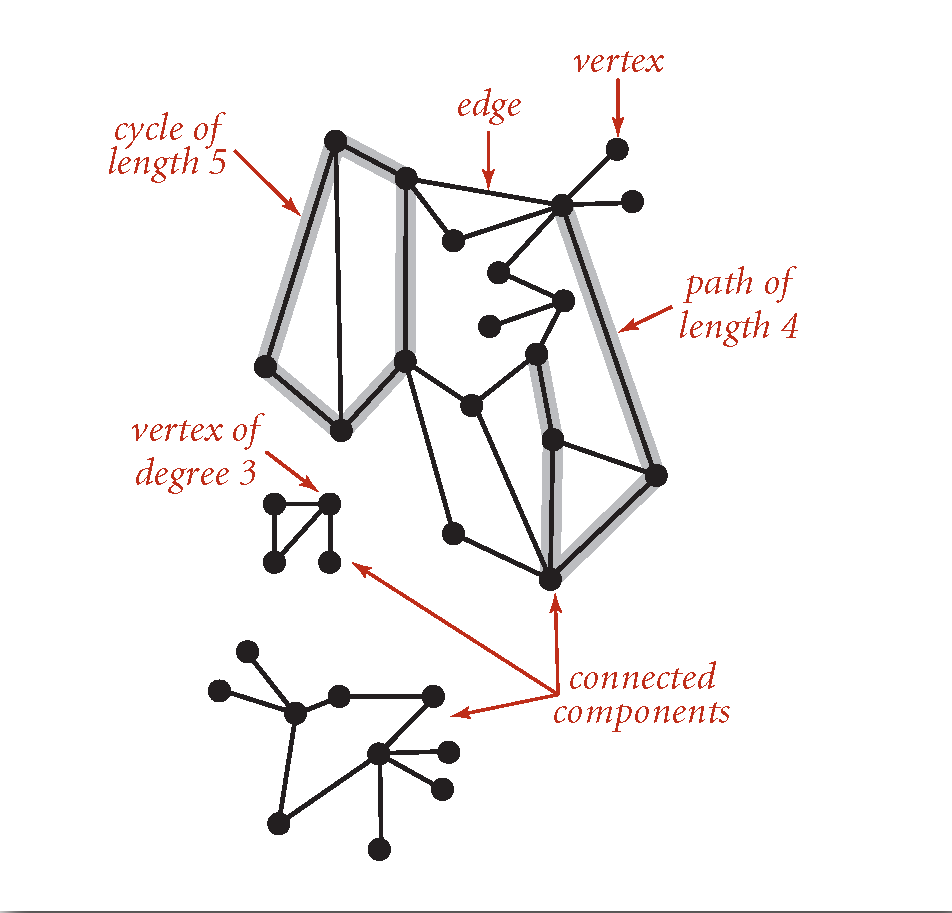
Graph: Set of vertices connected pairwise by edges.
Path: Sequence of vertices connected by edges.
Cycle: Path whose first and last vertices are the same.
Two vertices are connected if there is a path between them.
14.2 Graph API
Representation Types
Set-of-edges graph representation: Maintain a list of the edges (linked list or array).
Adjacency-matrix graph representation: Maintain a two-dimensional
adj[v][w] = adj[w][v] = true.Adjacency-list graph representation: Maintain vertex-indexed array of lists.
In practice: use adjacency-lists representation.
Algorithms based on iterating over vertices adjacent to
Real-world graphs tend to be sparse (huge number of vertices, small average vertex degree).
14.3 Depth-First Search
Goal: Systematically search through a graph.
Typical applications
Find all vertices connected to a given source vertex.
Find a path between two vertices.
Depth-First Search
Mark vertex
Recursively visit all the unmarked vertices adjacent to
Properties
DFS marks all vertices connected to
After DFS, can find vertices connected to
14.4 Breadth-First Search
Breadth-First Search
Put s onto a FIFO queue, and mark s as visited.
Repeat until the queue is empty.
Remove the least recently added vertex v.
Add each of v's unvisited neighbors to the queue, and mark them as visited.
Property
BFS computes shortest paths (fewest number of edges) from s to all other vertices in a graph in time proportional to
Depth-first search: put unvisited vertices on stack.
Breadth-first search: put unvisited vertices on queue.
14.5 Connected Components
Connected Components: A connected component is maximal set of connected vertices.
Find all Connected Components
Mark vertex
Recursively visit all the unmarked vertices adjacent to
14.6 Important Questions
Q: Implement depth-first search in an undirected graph without using recursion.
A: Simply replace a queue with a stack in breadth-first search.
Given a connected graph with no cycles
Q: Diameter: design a linear-time algorithm to find the longest simple path in the graph.
A: to compute the diameter, pick a vertex
Q: Center: design a linear-time algorithm to find the center of the graph.
A: Consider vertices on the longest path.
Q: An Euler cycle in a graph is a cycle (not necessarily simple) that uses every edge in the graph exactly one. Design a linear-time algorithm to determine whether a graph has an Euler cycle, and if so, find one.
A: use depth-first search and piece together the cycles you discover.
15 Directed Graphs
15.1 Introduction to Directed Graphs
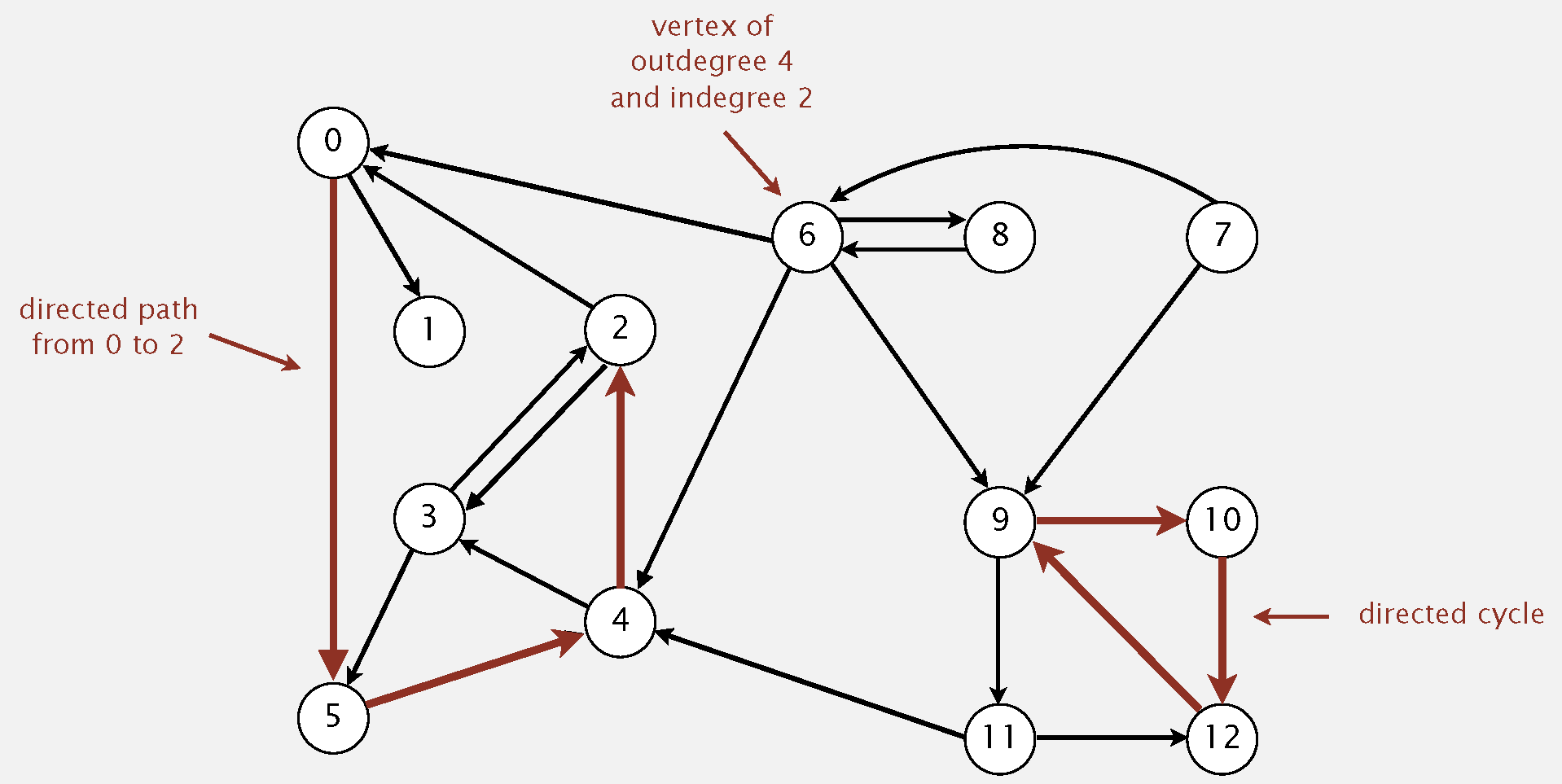
Directed graph: Set of vertices connected pairwise by directed edges.
15.2 Directed Graph API
15.3 Digraph Search
15.3.1 Depth-First Search for Digraph
15.3.2 Breadth-First Search for Digraph
Reachability application:
Program control-flow analysis
Mark-sweep garbage collector: if ao object is unreachable, it is garbage.
Application
Web crawler
15.4 Topological Sort
DAG: Directed Acyclic Graph.
Topological sort: Redraw DAG so all edges point upwards.
Property: A digraph has a topological order iff no directed cycle.
Application: Precedence scheduling, cycle inheritance, spreadsheet recalculation, etc.
15.4.1 Algorithm Ⅰ - Depth-First Search
Topological Sort with DFS
Run depth-first search.
Return vertices in reverse postorder.
15.4.2 Algorithm Ⅱ - Kahn's Algorithm
Topological Sort with Kahn's Algorithm
Calculate in-degrees.
Find nodes with in-degree 0.
Process nodes in topological order, and decrement in-degree of neighbors.
15.5 Strong Components
Connected Components | Strongly-Connected Components | |
|---|---|---|
Definition | ||
Implementation | DFS | DFS & Reverse DFS |
Detail | 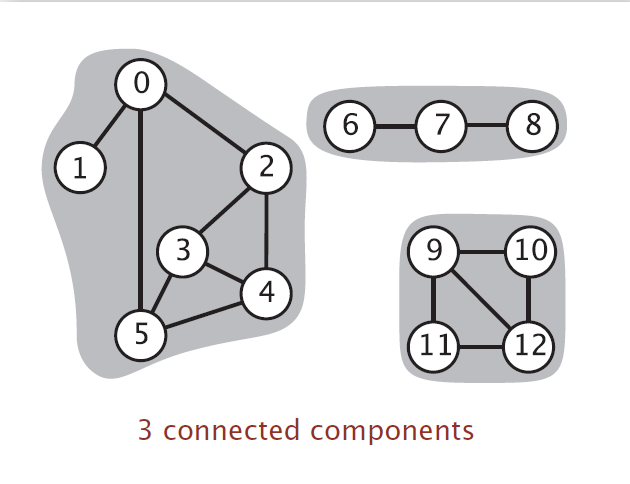 | 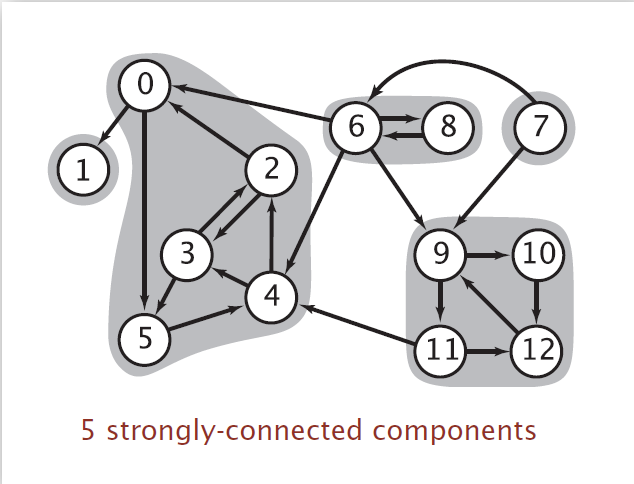 |
Strongly-Connected Components
Computer topological order (reverse postorder) in kernel DAG.
Run DFS, considering vertices in reverse topological order.